Roots and Optima Examples
10.5 Specific heat
Engineers use thermodynamics in their work to precisely heat and cool solids, liquids and gases. The following equation relates the zero-pressure specific heat of dry air \(c_p\) [kJ/(kg K)] to temperature [K]:
\[c_p = 0.99302 + 1.672 \times 10^{-4}T + 9.7216 \times 10^{-8}T^2 - 9.5837 \times 10^{-11}T^3 +1.9320 \times 10^{-14}T^4\]
Make a plot of \(c_p\) versus temperature from \(T = 0\) to 1200 K. Then, find the temperature that corresponds to a \(c_p\) of 1.1 kJ/(kg K).
# define our variables
A_0 <- 0.99302
A_1 <- 1.672E-4
A_2 <- 9.7216E-8
A_3 <- -9.5837E-11
A_4 <- 1.9320E-14
T_range <- seq(0,1200, by = 1)
c_p0 <- 1.1
# define our function
c_p <- function(T_K, A_0, A_1, A_2, A_3, A_4, c_p0){
A_0 + A_1 * T_K + A_2 * T_K^2 + A_3 * T_K^3 + A_4 * T_K^4 - c_p0
}
plot(T_range, c_p(T_K = T_range, A_0 = A_0, A_1 = A_1, A_2 = A_2, A_3 = A_3, A_4 = A_4, c_p0 = 1.1))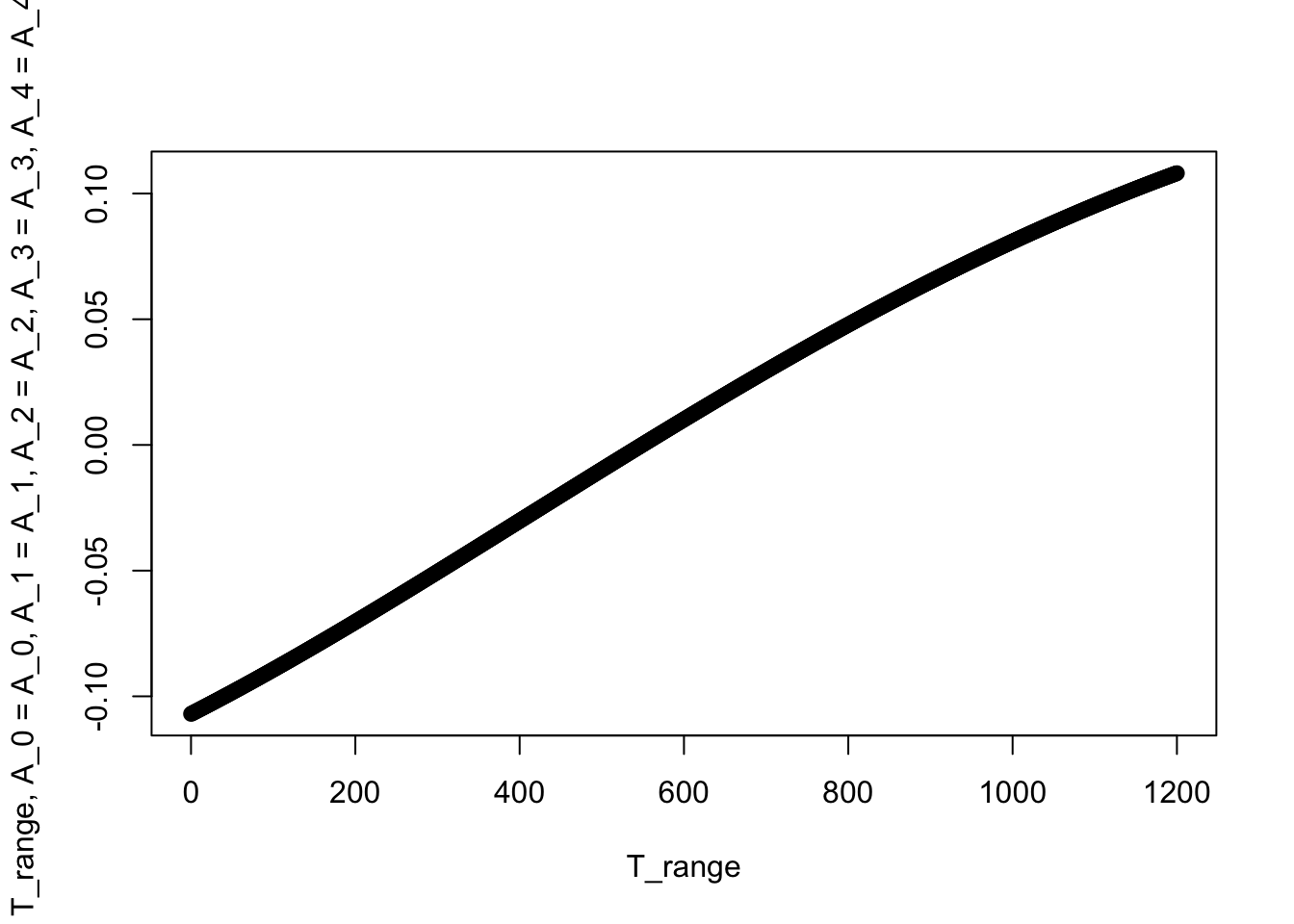
uniroot(f = c_p, interval = c(0, 1200), A_0 = A_0, A_1 = A_1, A_2 = A_2, A_3 = A_3, A_4 = A_4, c_p0 = c_p0)## $root
## [1] 548.946
##
## $f.root
## [1] 1.309735e-10
##
## $iter
## [1] 5
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-0510.6 Channel perimeter
As a Biological Systems Engineer, imagine you are asked to design a trapezoidal channel to carry irrigation water. Determine the optimal dimensions to minimize the wetted perimeter for a cross-sectional area of 50 m2.
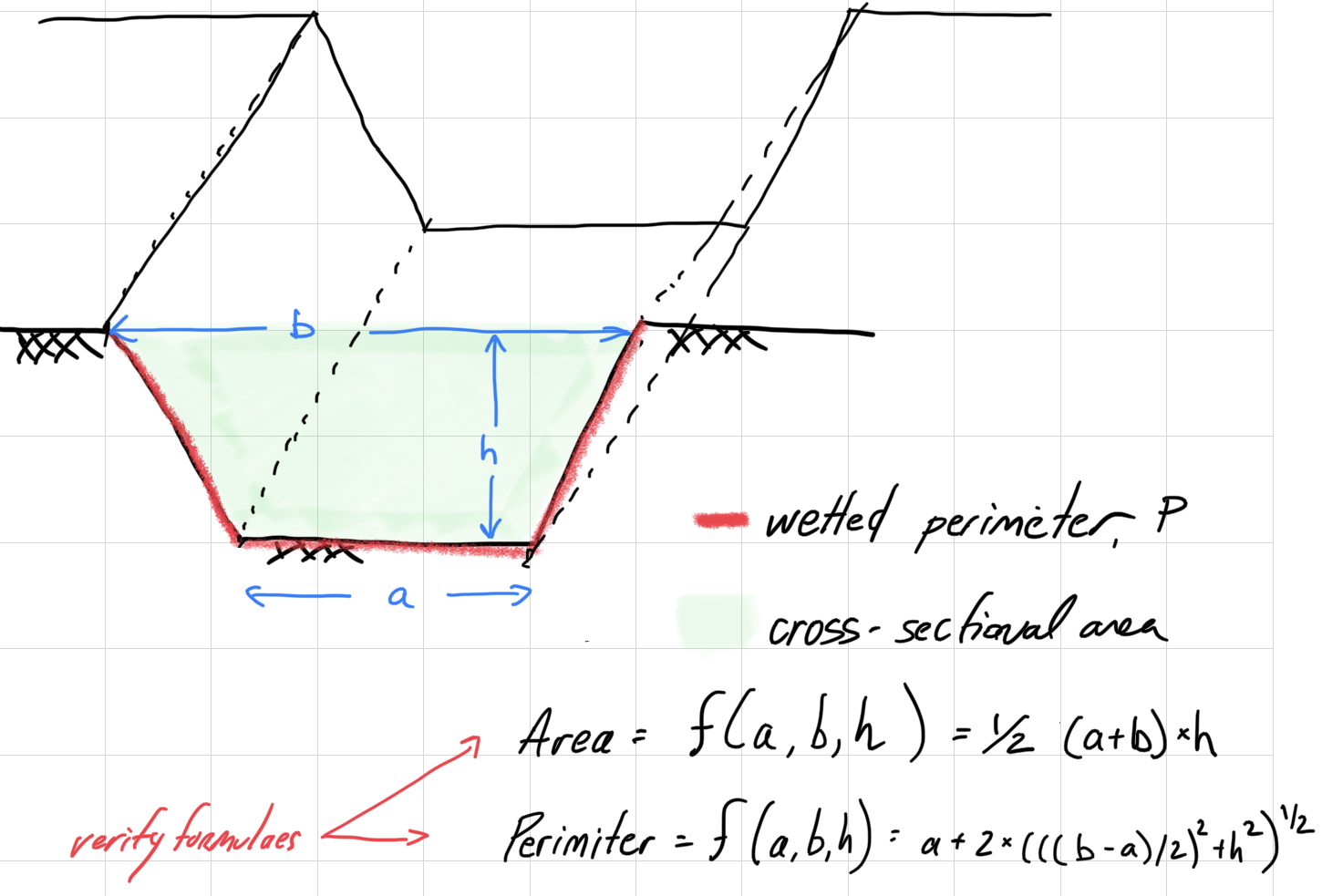
\[P = a + 2 \sqrt{\left(\frac{b-a}{2}\right)^2 +h^2}\] \[A = \frac{1}{2} \left(a + b \right) h\] \[50 = \frac{1}{2} \left(a + b \right) h\] Solve for h. \[h = \frac{100}{\left(a + b \right)}\]
Plug into perimeter function.
\[P = a + 2 \sqrt{\left(\frac{b-a}{2}\right)^2 +\left( \frac{100}{\left(a + b \right)} \right)^2}\] #### Plot equation
## Loading required package: ggplot2##
## Attaching package: 'plotly'## The following object is masked from 'package:ggplot2':
##
## last_plot## The following object is masked from 'package:stats':
##
## filter## The following object is masked from 'package:graphics':
##
## layoutlibrary(pracma)
a <- seq(1,50,0.1) # define range in a values
b <- seq(1,50,0.1) # define range in y values
ab <- pracma::meshgrid(a,b) # create grid of x,y pairs to evaluate
# NOTE: meshgrid takes two vectors and makes a matrix of all pairs of these values and renames these values X and Y
## a = ab$X b = ab$Y
P <- ab$X + 2 * sqrt(((ab$Y-ab$X)/2)^2 +(100/(ab$X + ab$Y))^2)
# use grid to create Z values (3rd dimension)